Modulo to the Resuce
One of the problems on KernelBench that Tensara poses as a challenge is the Argmax of a Tensor. Simply put, we find the index of the maximum element in dim d and reduce the array along that dimension, replacing multiple values with the index. Sounds confusing ? Here is a visualization to help you:
>>> A
tensor([[[35, 21, 24, 11],
[ 8, 48, 39, 48],
[10, 42, 20, 16]],
[[16, 37, 6, 46],
[40, 44, 44, 47],
[31, 7, 40, 10]]])
>>> A.argmax(dim=0)
tensor([[0, 1, 0, 1],
[1, 0, 1, 0],
[1, 0, 1, 0]])
>>> A.argmax(dim=1)
tensor([[0, 1, 1, 1],
[1, 1, 1, 1]])
>>> A.argmax(dim=2)
tensor([[0, 1, 1],
[3, 3, 2]])In each of the argmax calculations, we went from a 3-D to a 2-D tensor, replacing a row or a column of values with a single one
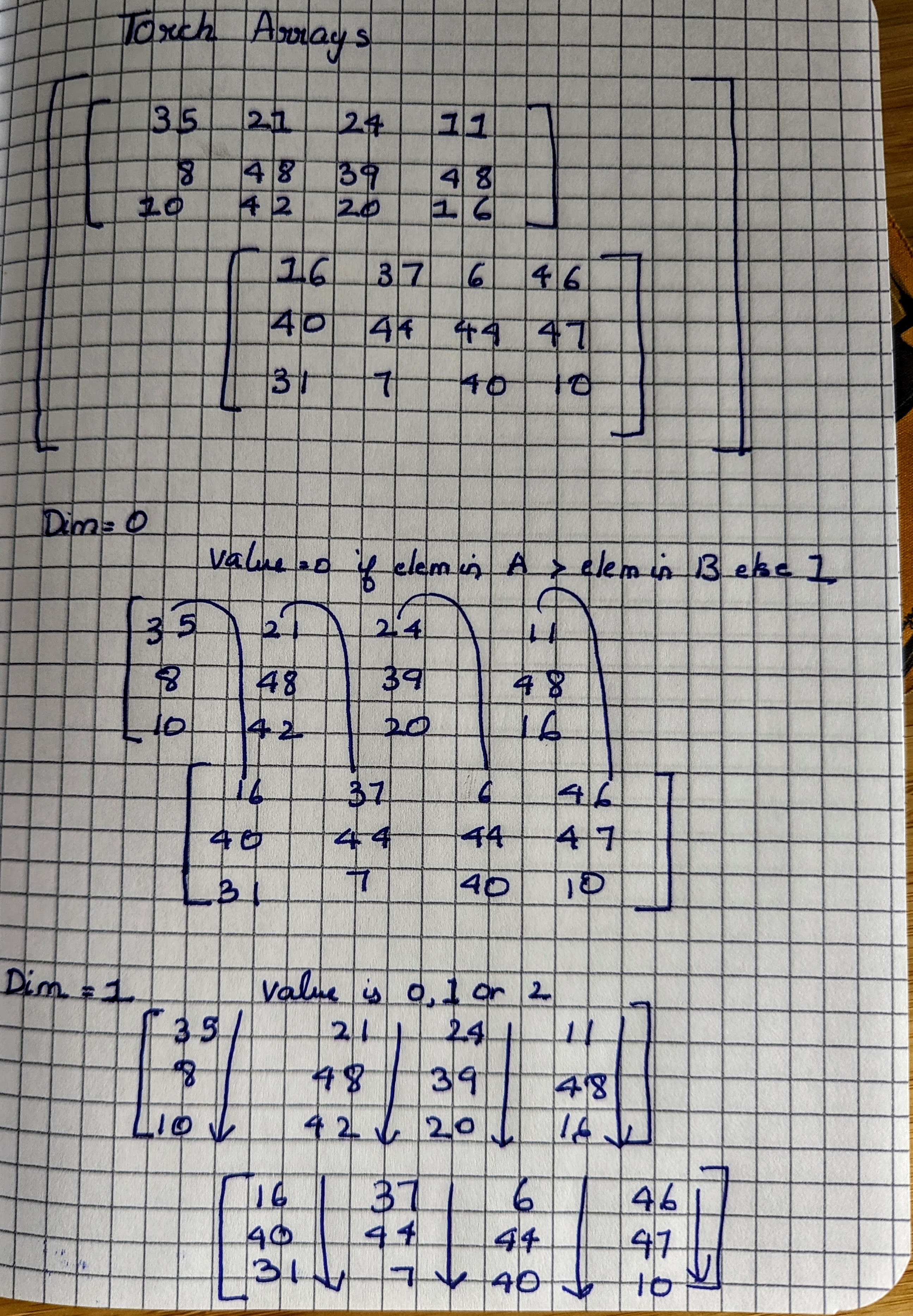
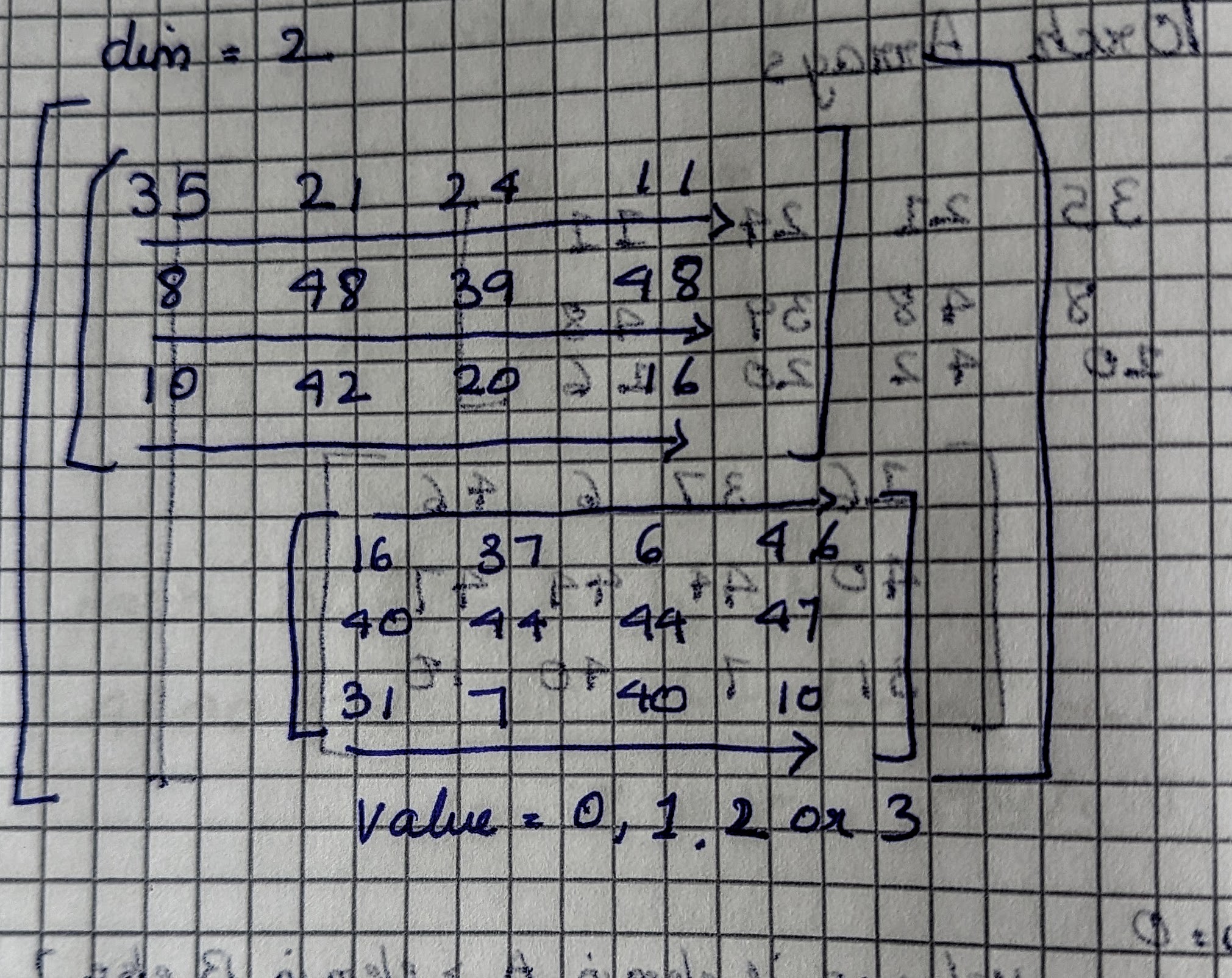
This is the visualization of a 3-D dimensional Tensor. Dim 0 is one of the 2 2-D matrices, Dim 1 are columns and Dim 2 are the rows.
To calculate Argmax across Dim 1 (the column), we find the largest element in A[n][i][0], A[n][i][1], A[n][i][2], A[n][i][3], where n is [0..1], i is [0..2]
So how can we parallelize calculating argmax via CUDA ?
Note that my kernel might not be the most optimal implementation, but I still found the algorithm interesting enough to write a blog post about it.
To effectively parallelize, let’s figure out how many threads we must launch and what memory addresses the thread must read and update to calculate the argmax.
From the image above, what happens if we chose dim=1 to calculate Argmax ? Since we are calculating an argmax per column and there are 4 columns in each of A[0] & A[1], we will calculate 2x4 = 8 values of shape (2, 4).
Let’s choose dim=2, that is calculating argmax per row. With 3 rows in each of A[0] and A[1], we calculate 2x3=6 values of shape (2, 3)
With dim=1, we compare A[0][0][0] with A[1][0][0], A[0][0][1] with A[1][0][1] and thus endup calculating 3x4=12 values of dim (1, 12).
Notice a pattern? For argmax along dim d (where d is 0, 1 or 2), we simply remove shape[d] and multiply the remaining sizes in the shape array. For A, with shape = (2, 3, 4), argmax along dim=1 is shape[0]*shape[2], for dim=2: shape[0]*shape[1] and for dim=3: shape[1]*shape[2]
Great, now we know how many values to calculate, we can launch a CUDA thread for each output value to be calculate. What are the input locations then that each thread must compare to find the argmax ?
For argmax along a specific dimension of a tensor, we’re essentially:
- Breaking the tensor into “slices” perpendicular to our target dimension
- Processing each slice independently
I found the algorithm hard to understand without a concrete example, so let’s start with an example and generalize it into an algorithm.
Let’s apply our algorithm to a 5D tensor with shape [2, 3, 4, 5, 6] and argmax over dimension 2
The first thing we do is to calculate the stride for each of the dimensions, starting from the last one (dim=4). Since the data in the memory is laid out as a 1-D array, the stride of dim d will tell us how many elements we will jump if we increment the value by 1. For dim=4, stride[4] = 1, as everytime we jump, we move to the next element (think of a jump as moving from column 1 -> 2 in the same row).
For dim=3, stride[3]=shape[4] (think of this as moving from one row to the next, we move by the number of elements / row).
For dim=2, stride[3]=shape[3]*stride[4] (think of this as jumping from one 2-D matrix to the next)
Starting stride[n-1] = 1,
Generalizing, we can calculate stride[i]= shape[i]*stride[i+1] going from i=n-2..0
Next up we calculate weights. The weights are used later to map the 1-D index of a CUDA thread to the corresponding multi-dimensional index in the input tensor. The calculation of weights is similar to calculating the stride, except we skip over the dimension along which we are calculating the Argmax
// dim is the dimension we are calculating argmax over
// Calculate weights for dimension mapping
int* h_weights = new int[ndim];
int running_weight = 1;
// Process from right to left, skipping the target dimension
for (int i = ndim-1; i >= 0; i--) {
if (i == dim) {
h_weights[i] = 0; // Not used for the target dimension
continue;
}
h_weights[i] = running_weight;
running_weight *= h_shape[i];
}For Argmax(dim=2), our h_weights array will look like this : [90, 30, 0, 6, 1]
Why is the h_weights array value calculated as such, especialy with h_weights[dim] = 0 ? Each CUDA thread will find the max of all the shape[dim] values. Inside the kernel, we will plug the value of i ranging from 0..shape[dim-]-1 in a loop to calculate the index of each element that the thread will be comparing.
Also, note that there are fewer threads that the number of elements since we “remove” shape[dim] before calculating threads=prod(shape). Therefore the weights array will help each thread calculate the right multi-dimensional index in a dimensional space where dim is removed from shape
Let us continue using the example above:
Total elements: 2 × 3 × 4 × 5 × 6 = 720
Elements along dimension 2: 4
Number of slices: 720 ÷ 4 = 180
Let’s map thread ID 42 to 4D indices (excluding dimension 2). Recall that h_weights = [90, 30, 0, 6, 1]
We are launching a 1-D thread grid of 1-D thread blocks. We thus have a linear thread index and we derive the index in each dimension to help us iterate over the input array (and store it in the array indices)
We start with the linear index of the thread as the remainder and for each dimension, calculate its position by
- Dividing by the “weight” of each dimension
- Taking the remainder for the next division
For dim 0: 42 ÷ 90 = 0 remainder 42
For dim 1: 42 ÷ 30 = 1 remainder 12
For dim 3: 12 ÷ 6 = 2 remainder 0
For dim 4: 0 ÷ 1 = 0 remainder 0
This is exactly like converting between number systems, where each position has a different “base” (the size of the dimension).
From here, it is easy to calculate the 1-D index of each element that a thread must access and compare to calculate the Argmax.
// Find the maximum value along the specified dimension
float max_val = -INFINITY;
int max_idx = -1;
// Iterate through all positions along the target dimension
for (int i = 0; i < shape[dim]; i++) {
// Set the index for the dimension we're iterating over
indices[dim] = i;
// Calculate the flat index into the input array
int flat_idx = 0;
for (int j = 0; j < ndim; j++) {
flat_idx += indices[j] * strides[j];
}
// Check if this value is larger than our current max
if (input[flat_idx] > max_val) {
max_val = input[flat_idx];
max_idx = i;
}
}I tried to write down a paragraph to explain how this loop works, but I will be admit that I cannot describe it in words very well. The best explanation is something like this, if you are comparing along dim=2, then each element you have to compare is shape[3]*shape[4] elements away from one another. We used the generic formula position = i₁ × (D₂ × D₃ × ... × Dₙ) + i₂ × (D₃ × ... × Dₙ) + ... + iₙ where i is the value of each dim in the indices array that we calculated for each thread.
I urge you to use Claude or any LLM and sit and work this with a pen and paper as drawing shapes on paper is worth 10,000 or more digital characters.
Storing the output is straight forward. Since we reduce the output size to prod(shape)/shape[dim] outputs, each thread thus outputs only one value (after iterating over shape[dim] values). Thus the kernel’s final output is
// Iterate over the dimension we're reducing
for (int i = 0; i < shape[dim]; i++) {
...
}
output[tid] = max_idx;Conclusion
This was a fun kernel exercise for me. It took me a few days of figuring out (and dealing with a stupid size calculation bug that was giving incorrect outputs for a long while before I fixed it) and I sat on writing this article for a long time due to other commitments. I am pasting the entire program in this post (as the leetgpu snippet sharing feature isn’t working yet). If you find any bugs or an improved algorithm, please do reach out to me as I am always on the lookout for advice from CUDA kernel programming masters
#include <cuda_runtime.h>
#include <stdio.h>
#define MAX_DIM 16
#define TOTAL_SIZE 2*3*4
__global__ void argmax(const float* input, int dim, int* output, int* shape, int ndim, int* strides, int* weights, int slices) {
int tid = blockDim.x * blockIdx.x + threadIdx.x;
if (tid >= slices) { return; }
// Initialize indices for this particular slice
int indices[MAX_DIM];
for (int i = 0; i < ndim; i++) {
indices[i] = 0;
}
// Convert linear index to multi-dimensional indices
int rem = tid;
for (int i = 0; i < ndim; i++) { // Note: forward order
if (i != dim) {
int idx_i = rem / weights[i];
indices[i] = idx_i;
rem %= weights[i];
}
}
// Find the maximum value along the specified dimension
float max_val = -INFINITY;
int max_idx = 0; // Default to first element
// Calculate the base flat index for this slice (excluding the dimension we're maxing over)
int base_idx = 0;
for (int j = 0; j < ndim; j++) {
if (j != dim) {
base_idx += indices[j] * strides[j];
}
}
// Iterate over the dimension we're reducing
for (int i = 0; i < shape[dim]; i++) {
// Calculate flat index - base index plus offset in the dimension we're iterating
// int flat_idx = base_idx + i * strides[dim];
int flat_idx = base_idx + i * strides[dim];
// Find maximum
if (input[flat_idx] > max_val) {
max_val = input[flat_idx];
max_idx = i; // Store the index along dim dimension
}
}
output[tid] = max_idx;
}
// Note: input, output, shape are all device pointers to float32 arrays
void solution(const float* input, int dim, int* output, int* shape, int ndim) {
// Calculate strides (how many elements to move for each dimension)
int* h_strides = (int*) malloc(ndim * sizeof(int));
h_strides[ndim-1] = 1;
for (int i = ndim-2; i >= 0; i--) {
h_strides[i] = h_strides[i+1] * shape[i+1];
}
// Calculate total number of slices (elements in the output)
int slices = 1;
for (int i = 0; i < ndim; i++) {
if (i != dim) {
slices *= shape[i];
}
}
int* h_weights = (int*) malloc(ndim * sizeof(int));
for (int i = 0; i < ndim; i++) {
h_weights[i] = 0;
}
int weight = 1;
for (int i = ndim-1; i >= 0; i--) {
if (i != dim) {
h_weights[i] = weight;
weight *= shape[i];
}
}
// Allocate and copy device memory
int *d_strides = 0;
int *d_weights = 0;
cudaMalloc((void**)&d_strides, sizeof(int) * ndim);
cudaMemcpy(d_strides, h_strides, sizeof(int) * ndim, cudaMemcpyHostToDevice);
cudaMalloc((void**)&d_weights, sizeof(int) * ndim);
cudaMemcpy(d_weights, h_weights, sizeof(int) * ndim, cudaMemcpyHostToDevice);
// Launch kernel
int threadsPerBlock = 256;
int numBlocks = (slices + threadsPerBlock - 1) / threadsPerBlock;
argmax<<<numBlocks, threadsPerBlock>>>(input, dim, output, shape, ndim, d_strides, d_weights, slices);
cudaDeviceSynchronize();
// Free memory
cudaFree(d_strides);
cudaFree(d_weights);
free(h_strides);
free(h_weights);
}
int main() {
float* h_input = (float*)malloc(sizeof(float)*TOTAL_SIZE);
for(int i=0;i<(TOTAL_SIZE);i++) {
h_input[i] = (float)i;
}
int h_shapes[] = {2, 3, 4};
float* d_input = 0;
int* d_output = 0;
int* d_shapes = 0;
int items = 2*4;
cudaMalloc((void**)&d_input, sizeof(float)*TOTAL_SIZE);
cudaMemcpy(d_input, h_input, sizeof(float)*TOTAL_SIZE, cudaMemcpyHostToDevice);
cudaMalloc((void**)&d_output, sizeof(float)*items);
cudaMalloc((void**)&d_shapes, sizeof(h_shapes));
cudaMemcpy(d_shapes, h_shapes, sizeof(h_shapes), cudaMemcpyHostToDevice);
solution(d_input, 1, d_output, d_shapes, 3);
int* output = (int *)malloc(sizeof(int)*TOTAL_SIZE);
cudaMemcpy(output, d_output, sizeof(int)*items, cudaMemcpyDeviceToHost);
for(int i=0;i<items;i++) {
printf("%d ", output[i]);
}
}